Design of shear wall

Design of shear wall:

The vertical structural element of a reinforced concrete framed structure which is provided to resist in-plane lateral loads is known as shear wall. The design of shear wall is necessary to resist the in-plane shear and in-plane flexural moment caused by lateral loads through the vertical cantilever Action. Here we discuss about the design of shear wall located around the lift.

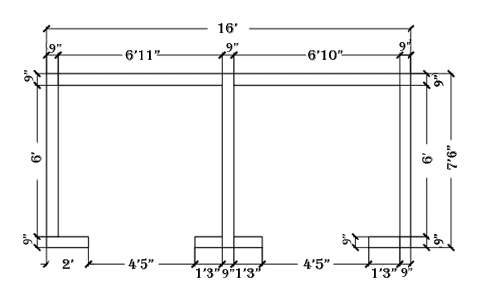
Design a shear wall of a building which is located in three side if the lift as shown. Grade of concrete = M25 and grade of steel = Fe 500

• 

Total length of the wall = 192 + 90*3+15*4+9*2= 549 in. = 13.9446 m.

Floor height = 3.2004 m.

Wall thickness = 9 in. = 0.2286 m.

The stepwise design of shear wall procedure is as follows:

Check for slenderness ratio:

Eff. Height of wall, he = 0.75H = 0.75*3.2004 = 2.4003m

Slenderness ratio, he/t = 2.4003/0.2286 = 10.50 < 30 OK.

Min. eccentricity, E min = e = 0.05t (Clause 32.2.2, IS 456:2000)

= 0.05*0.2286=0.01143m = 11.43mm

Additional eccentricity (ea) = he2/2500t

= 2.40032/ (2500*0.2286) = 0.010813m = 10.813 mm

Calculation of load:

1. Ground floor:

Length = 13.9446 m

Height =2.798/2+3.2004/2 = 2.9992m.

Load = 25*13.9446*2.9992*0.2286 = 239.01 KN

2. Typical Floor:

Length = 13.9446 m

Height = 3.2004/2+3.2004/2 = 3.2004 m

Load = 25*13.9446*3.2004*0.2286 = 255.05 KN

3. Second last Floor:

Length = 13.9446 m.

Height = 3.2004/2+2.8956/2 = 3.048m.

Load = 25 * 13.9446 * 3.048 * 0.2286 = 242.90 KN

4. Top Floor:

Length = 13.9446 m

Height = 2.8956/2 = 1.4478

Load = 25*13.9446*1.4478*0.2286 = 115.3808 KN

Roof load:

Plan area = 192” * 90” = 4.8768 m * 2.286 m = 11.1483 m2.

Slab thickness = 150 mm = 0.15 m

Slab load = 11.1483*0.15*25 = 41.80 KN.

Total Top Floor Load = 115.3808 + 41.80 =157.18 KN

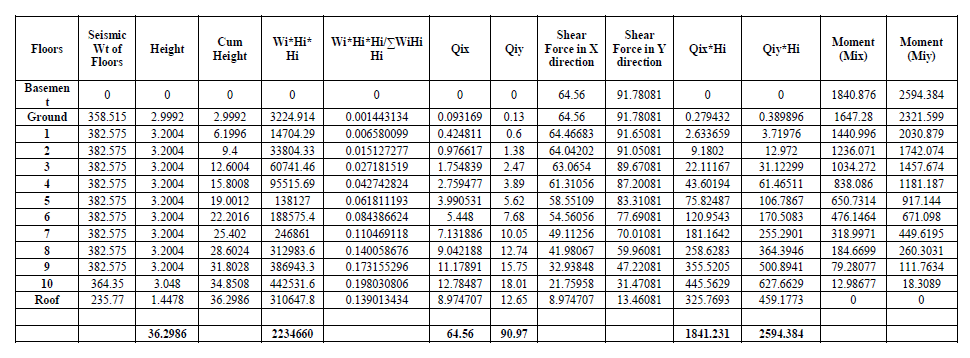
Total load = 239.01+9*255.05+242.90+157.18 = 2934.54 KN

Calculation of base shear:

Total seismic weight of lift (W) = 2934.54 KN

Height, h = 37.698m

Base shear, V_b = A_h*W (Clause 7.5.3, IS 1893 (Part 1) : 2002)

Where,

A_h = design horizontal acceleration spectrum

W = seismic weight as per (Clause 7.4.2, IS 1893 (Part 1) : 2002)

Now, A_h = 𝑍𝐼𝑆_a/2𝑅𝑔 (Clause 6.4.2, IS 1893 (Part 1) : 2002)

Where,

Z = zone factor = 0.36 for Seismic Zone V (Table 2, IS 1893 (Part 1) : 2002)

I = importance factor = 1 (Table 6, IS 1893 (Part 1) : 2002)

R = response reduction factor=5 (Table 7, IS 1893 (Part 1) : 2002)

S_a/g = average response acceleration coefficient

Width of Shear wall:

D_Y = 4.8768 m.   

D_X = 2.2860 m

Time Period (TA) = 0.09ℎ√𝑑 (Clause 7.6.2, IS 1893 (Part 1) : 2002)

TAy = 0.09∗37.698√4.8768

=1.53 sec.

TAx = 0.09∗37.698√2.2860

= 2.24 sec.

For soil type of type II

For TAy =1.53 sec.

(Sa/g)Y = 1.361.53 = 0.88

Ahy=0.36*1*0.88 / (2*5)

=0.031

Again, For TAx = 2.24 sec.

(Sa/g)X = 1.362.24 =0.607

Ahx =0.36*1*0.607 / (2*5)

=0.022

Now,

Base shear (Vby) = Ahy*W = 0.033*2934.54 = 90.97 KN

Base shear (Vbx) = Ahx*W = 0.022*2934.54 = 64.56 KN

The deign axial strength of a wall per unit length,

Puw = 0.3(t-1.2e-2ea) f_ck (Clause 32.2.5, IS 456 : 2000)

Where, t= thickness of the wall

e = eccentricity

ea = additional eccentricity due to slenderness effect taken as Hwe²/2500t.

Puw = 0.3(228.60-1.2*11.43-2*10.813)*25 = 1460.41 N/mm.

Calculation for main vertical reinforcement:

Assume clear cover 15 mm. and 12mm dia. bars.

When lateral load is acting along X – direction:

Mu/3 = 1.5∗1840.876/3 = 920.438 KNm

Vu/3= 1.5∗64.56/3 = 32.28 KN

Pu/3= 1.5∗2934.54 /3 = 1467.27 KN

d’/D = (15+6)/4876.80 = 0.0043. (Adopt 0.05)

Mu/fckbd² = 920.438*106/ (25*228.60*2286²) = 0.0308

Pu/fckbd = 1467.27*1000/ (25*2286*228.60) = 0.1123

Using chart 35 SP 16:

p/fck = 0.00

Check for minimum reinforcement:

Ast, min = 0.0025 * bD = 0.0025*228.60*2286 = 1306.45 mm2.

Ab = 𝜋 * 12²/4 = 113.0973 mm2

Spacing of bars = 2286 * 113.0973 / 1306.45 = 197.89 mm.

Check for spacing of bar

Spacing ≤ 3t or 450 mm whichever is less

=3*228.6 or 450mm

=685.8 or 450 OK

To take account of opposite phenomena, Provide 12 mm dia bar @ 180mm c/c on both sides.

When lateral force is acting along Y-direction

Mu= 1.5 * 2761.59 = 3891.576 KNm

Vu=1.5 * 96.381 = 136.455 KN

Pu= 1.5 * 2934.54 = 4401.81 KN

d’/D = (15+6)2286 = 0.0091. Adopt 0.05.

Mu/fckbd² = 3891.576*106/ (25*228.60*4876.80²) = 0.029

Pu/fckbd = 4401.81*1000/ (25*4876.80*228.60) = 0.157

Using chart 35 SP 16:

p/fck = 0

Ast, min = 0.0025*228.60*4876.80=2787.09mm2

Ab = π*12²/4 = 113.0973 mm2

Spacing of bars = 4876.80*113.0973/2787.09= 197.89mm

Check for spacing of bar

Spacing ≤ 3t or 450 mm whichever is less.

= 3*228.6 or 450 mm

= 685.8 or 450 OK

To take account of opposite phenomena, Provide 12 mm dia bar @ 180mm c/c on both sides.

Calculation of Horizontal steel reinforcement:

Area of horizontal steel reinforcement = 0.25% bH = 0.0025*228.60*3200.4 = 1829.0286 mm2.

Provide 12mm dia. bars.

Ab = π *12²/4 = 113.0973 mm2.

Spacing of bars = 3200.4*113.0973/1829.0286 = 197.90 mm.

Provide 12mm dia. bars @180mm c/c on both face.

Check for shear:

Along Y- direction (long wall):

As per Clause 32.4.2, IS 456 : 2000

Nominal shear stress, 𝜏_v = V_u/td

Where, V_u = Shear force due to design loads.

t = wall thickness.

d = 0.8 * Lw where Lw is the length of the wall.

Here, 𝜏v = Vu/ (t*0.8*Lw) = 144.57*103/ (228.60*0.8*4876.80) =0.162 N/mm2

Allowable shear stress, 𝜏a = 0.17fck = 0.17*25 = 4.25 N/mm2 > 𝜏v.

Design shear strength of concrete:

Hw/Lw = 3200.4/4876.80 = 0.6563 < 1.

𝜏_cw = (3.0-Hw/Lw) Kl √f_ck = (3.0-0.6563)*0.2*√25 = 2.34 N/mm2 > 𝜏v.

Hence safe.

Along X- direction (short wall):

As per Clause 32.4.2, IS 456 : 2000

Nominal shear stress, 𝜏_v = Vu/td

Where, Vu = Shear force due to design loads.

t = wall thickness.

d = 0.8 * Lw where Lw is the length of the wall.

Here, 𝜏v = Vu/td = Vu/ (t*0.8*Lw) = 96.84*103/ (228.60*0.8*2286)

= 0.2316 N/mm2

Allowable shear stress, 𝜏a = 0.17fck = 0.17*25 = 4.25 N/mm2 > 𝜏v.

Design shear strength of concrete

Hw/Lw = 3200.4/2286 = 1.4 > 1.

𝜏cw = (𝐻𝑤/𝐿𝑤+1)/(𝐻𝑤*𝐿𝑤−1) * K₂√fck = (1.4+1)/(1.4−1) *0.045*√25 = 1.35 N/mm2 > 𝜏v.

Hence safe.

Summary:

Vertical reinforcement:

Provide 12 mm dia bar @ 180 mm c/c on both sides along X-direction.

Provide 12 mm dia bar @ 180 mm c/c on both sides along Y-direction.

Horizontal reinforcement:

Provide 12mm dia. bars @180 mm c/c on both face.

Anchorage Length:

Ld + 10b_d = 0.87∗𝑓𝑦∗𝛷/4 𝜏_𝑏𝑑 + 10*12 = 0.87∗500∗12/4∗1.4∗1.6 + 10*12 = 702.59mm.