Table of Contents
Torsion in building structure:
Torsion is the condition of being twisted or turned. Torsion in building structure is defined as the deformation or the stress developed in the building when one end of a member/structure is twisted in one direction and other end is held motionless or twisted in opposite direction or also in same direction but with less magnitude.

source: posted by Abdullah khan in Instagram
Torsional stiffness:
The torsional stiffness KT of a member is defined as the torsional moment T required to produce a unit angle of twist.
KT = T/Ѳ = GJ/L
T/J = GѲ/L = Ⴀt,max/R
Ⴀt,max = TR/J
Where,
J = Polar MOI of cross sectional
G = Shear modulus = E / 2(1 + μ)
E = Young’s modulus of elasticity
μ = poisson’s ratio
L = length of a member
For a rectangular section subjected to pure torsion, the maximum shear occur at the middle of the wider (or longer) side D and given by,
Ⴀt,max = T/ (K b2 D)
Where,
K b2 D = polar or torsional section modulus
b and D are the shorter and longer sides of the rectangular section, respectively
K = torsion constant
The value of k depend upon the ratio D/b and given in table:
Table: Variation of coefficient k with the ratio D/b
| D/b | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 4.0 | 5.0 | 6.0 | 8.0 | 10.0 | > 10 |
| K | 0.2 | 0.23 | 0.24 | 0.25 | 0.26 | 0.28 | 0.29 | 0.29 | 0.30 | 0.31 | 0.33 |
Torsional Irregularity:
Normally, a well-proportioned building does not twist about its vertical axis, when a) the stiffness distribution of the vertical elements resisting lateral loads is balanced in plan accordance to the distribution of mass in plan at each storey level and b) the floor slab is stiff in their own plane, happens when its plan aspect ratio is less than 3.
A building structure is said to be torsional irregular when 1) the maximum horizontal displacement of any floor in the direction of the lateral force at one end of the floor is more than 1.5 times its minimum horizontal displacement at the far end of the same floor in that direction; and 2) the natural period corresponding to fundamental torsional mode of oscillation is more than those of first two translational modes of oscillation along each principle plan directions.
In torsional irregular building, when the ratio of maximum horizontal displacement at the end corner of the building and the minimum horizontal displacement at the other end corner of the building is,
- In the range of 1.5 – 2.0
a) the building configuration should be revised to ensure that the natural period of fundamental torsional mode of oscillation shall be smaller than those of the first two translation modes along each of the principle plan directions, and then
b) three dimensional dynamic analysis method shall be adopted; and
2. More than 2.0, the configuration of the building shall be revised.
This provision is based on the IS code mentioned in 1893 (part 1) : 2016
Behavior of structure under torsion:
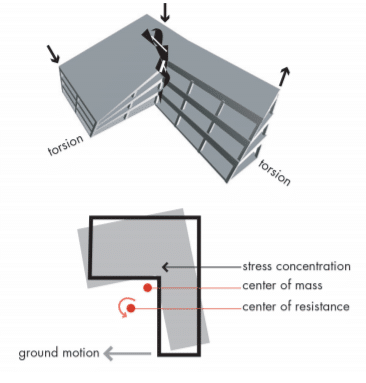
Cause of torsion in building structure:
- Reentrant Corner
A building is said to have a re-entrant corner in any plan direction, when its structural configuration in plan direction, when its structural configuration in plan has projection of size greater than 15% of its overall plan dimension in that direction.
source:https://www.awc.org
2. Unequal Mass distribution
The building having heavy mass in one area that other than other end the building may undergo torsional moment. For example, if the one side of a building has library, heavy instrument/devices and other end has very low mass, then the heavy end side undergoes more deflection than that of least mass.
3. Infill walls
The presence of infill wall in some area and absence in some area also cause torsion on building. It is almost similar to unequal mass distribution.
4. Position of Staircase or opening
The opening should be left in the slab for the casting of stairs. Opening in slabs results in flexural diaphragm behavior, and hence the lateral force is not shared by frames and/or vertical members in proportional to their lateral translational stiffness. A building is said to have discontinuous in their in-plane stiffness, when floor slabs have cut-outs or openings of area more than percent of the full area of the floor slab
Calculation of torsion in building:
The torsion in building is found out by measuring the distance between the center of mass and center of rigidity.
The max. Limit that the difference of center of mass rigidity can be is d > 20% of w, where w = width of building on that axis.
Torsional failure:
The failure of the building by torsion is severe so it is better to avoid it by revising the plan configuration. Three dimensional dynamic analysis method should be adopted to analyze the torsional effects.
ALSO READ:

