Isolated footing design

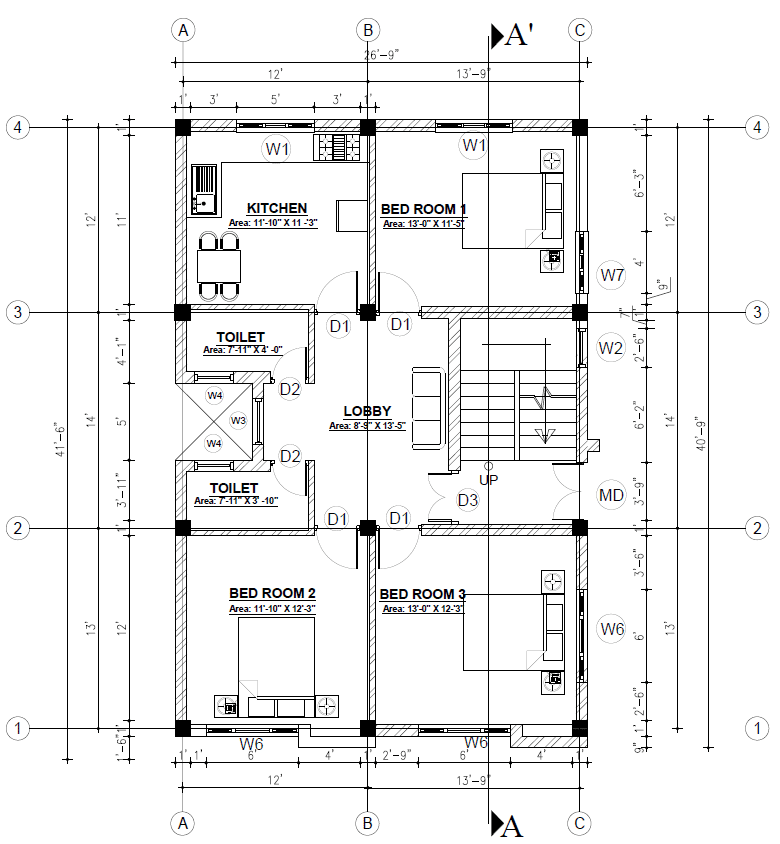
Design an isolated footing of the given building as shown:

Grade of concrete = 25 N/mm²;Grade of steel = 415 N/mm²

Column size = 1’ * 1’ = 305 mm * 305

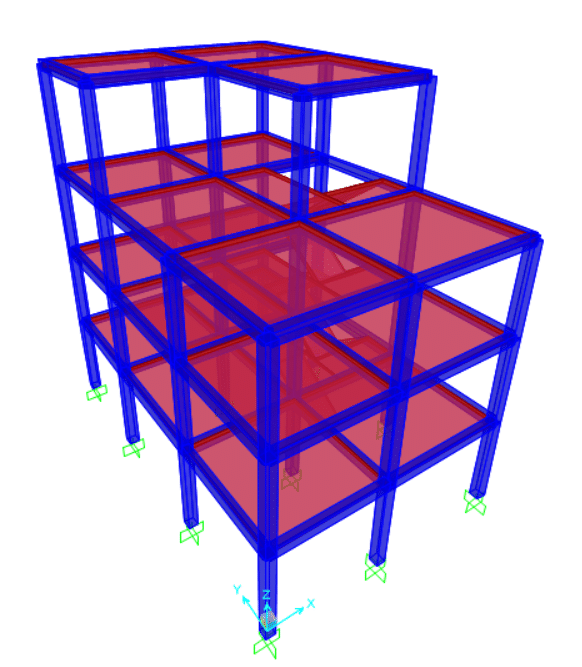
The structural design output value for isolated footing are:

Footing	Output Case	Case Type	Step Type	F3	M1	M2
	Text	Text	Text	KN	KN-m	KN-m
1	Envelope	Combination	Max	303.316	43.4039	42.769
1	Envelope	Combination	Min	87.055	-51.9247	-33.9018
2	Envelope	Combination	Max	458.315	43.011	44.8181
2	Envelope	Combination	Min	172.074	-51.2382	-41.2312
3	Envelope	Combination	Max	315.226	39.4609	33.146
3	Envelope	Combination	Min	107.46	-45.1896	-42.3828
4	Envelope	Combination	Max	458.035	52.7445	51.6481
4	Envelope	Combination	Min	167.229	-52.6878	-40.9427
5	Envelope	Combination	Max	846.577	52.7589	60.9906
5	Envelope	Combination	Min	413.799	-52.2924	-51.5955
6	Envelope	Combination	Max	682.623	53.8126	43.9389
6	Envelope	Combination	Min	222.274	-54.2414	-56.0346
7	Envelope	Combination	Max	582.917	54.1581	59.9258
7	Envelope	Combination	Min	190.899	-52.0849	-47.9118
8	Envelope	Combination	Max	864.837	54.042	63.1715
8	Envelope	Combination	Min	414.096	-51.179	-57.7312
9	Envelope	Combination	Max	674.645	82.5598	45.1608
9	Envelope	Combination	Min	255.531	-85.5023	-60.7769
10	Envelope	Combination	Max	421.182	51.94	64.3109
10	Envelope	Combination	Min	122.955	-43.831	-52.0679
11	Envelope	Combination	Max	621.05	52.8944	69.562
11	Envelope	Combination	Min	234.156	-42.7969	-62.085
12	Envelope	Combination	Max	444.272	50.2985	53.506
12	Envelope	Combination	Min	142.649	-38.8656	-59.2972

For design example, take the critical one. The footing 8 is critical since it has highest axial force and high value of moment.

From column, factored axial load = 864.37 KN and M_x = 54.042 KN-m and M_y = 63.1715 KN-m

Step 1: Calculate factored loads and bending moment

               The factored axial load and factored bending moment from the column is obtained from the structural software. Add 10% for self-weight of footing and soil above the footing.

 Factored axial load on footing = factored axial load from column + self-weight of footing

                                                            = 1.1 * 864.37

                                                            = 950.8 KN

The eccentricity is calculated as,

Eccentricity on x-axis = M_x/P = 54.042/864.37 = 0.0625 m = 62.5mm

Eccentricity on y-axis = M_y/P = 63.17 / 864.37 = 0.073 = 73 mm

               For simplicity in construction and supervision, it is better to increase the thickness of footing rather than shifting but it makes the structure little bit uneconomical. It is compulsory to go for non-shifting case if there is possibility of moment reversal.

Here we discuss about the only non-shifting case of isolated footing.

Step 2: Calculate an area of footings based on the factored axial load

               Area of footing = service load / safe bearing capacity of soil

Service load = factored load / factor of safety = 950.8 / 1.5 = 633.87 KN

Safe bearing capacity of soil = 150 kN/m²

so, area of footing = 633.87 / 150 = 4.226 m²

Adopt square footing

 L =B = √4.226 = 2.055m = 2055 mm

Take size of isolated footing = 2200 mm * 2200 mm

Step 3: Calculate critical bending moment:

The critical section for the bending moment is taken at the edge the column in case of column footing.

In Non-Shifting case, the ultimate soil pressure varies uniformly over the area of footing.

Ultimate soil pressure P_u = design load / area of footing * (1± 6e/(B or L))

                                             = 950.8 / 2.2² *( 1 ± 6 * 73/ 2200)

                                             = 235.56 KN/m²; 157.36 KN/m²

For one edge, + sign is used and for other side – sign is used depending upon position of eccentricity. But for design it okey to take any one side of the footing because there may be case of moment reversal in the building.

Find the maximum soil pressure P_u,max and soil pressure at the edge of column P_{ux or y}, then the  moment should be calculated on both axis.

P_u,max = 235.56 KN/m²

P_uy = 235.56 – (235.56 – 157.36)/ 2.2 * (2.2-0.305)/2

= 201.88 KN/m²

P_{uy,avg = ½ *} (P_u,max + P_uy)

               = (235.56 + 201.88)/2 = 218.72 KN/m²

For moment calculation, first take average of P_u,max  and P_{ux or y} then

M_uy = ½ P_uy,avg *B ( 0.5 L – 0.5l)² 

= ½ * 218.72 * 2.2 (0.5 * 2.2 – 0.5 * 0.305)²

= 216 KN-m

M_u is max. of M_ux  and M_uy

L and B is for footing and l and b for column

Step 4. Thickness of Footing

The thickness of footing is calculated from the maximum critical bending moment.

D_req. = √ (M_u / 0.138 f_ck B)

               = √ (216 * 10⁶ / 0.138 * 25 * 2200)

               = 168.7 mm

Increase depth for 1.75 to 2 times more than calculated value for shear considerations [This is done just to decrease the possibility of shear failure of footing while checking]

i.e. d = (1.75-2) D_req

                    = 2*168.7 = 337.4 mm

Adopt thickness of footing equal to 340 mm.

The value of d is the effective thickness of footing. For overall thickness, clear cover and half of diameter of reinforcement should be added.

Step 5: Calculation of reinforcement

The reinforcement is calculated from the critical maximum moment obtained in the step 4

M_u = 0.87 f_y A_st [ d – f_y* A_st / f_ck*b]

216 * 10⁶ = 0.87 * 415 * A_st [ 340 – 415 * A_st / 25 * 2200]

A_st = 1834.24 mm²

Provide 12 mm diameter of bar.

Area of a bar A_st1 = pi * 12²/4 = 113.1 mm²

Spacing of bar S = A_st1 * B /A_st = 135.65 mm

Provide spacing of 130 mm

Area provided = Ast1*B / S = 113.1 * 2200/130 = 1914 mm²

Percentage of reinforcement provided = A_st / Bd * 100 = 1914 * 100 / 2200*340

                                             = 0.255 %

The area of reinforcement is greater than 0.12% of Bd., OK

Step 6. Check for one way shear

The critical section is taken at a distance d away from the face of column.

P_u,max = 235.56 KN/m²

At critical section, ie at d distance from edge of column

P_uy = 235.56 – (235.56 – 157.36)/ 2.2 * (2.2-0.305- 2*340)/2

= 213.96 KN/m²

P_{uy,avg = ½ *} (P_u,max + P_uy)

               = (235.56 + 213.96)/2 = 224.76 KN/m²

Shear force per meter, V_u = P_u,avg * B *{0.5(L-l) – d}

                                             = 224.76 * 2.2 * [0.5 (2.2 – 0.305) – 0.34]

                                             = 300.4 KN

Since the footing is square so the shear stress is same for both axis.

Nominal shear stress Ʈ_u = V_u /Bd

                                             = 300.4 / 2.2 * 0.34

                                             = 401.6 KN/m²

                                                            = 0.4 N/mm²

The nominal shear stress should be less than shear strength of the footing, that is

Shear strength Ʈ_uc = k Ʈ_c

The value of k depend up on the thickness of footing which can be obtained from clause 40.2.1.1 of IS code 456:2000

K = 1 [For depth more than 300 mm]

And the value of Ʈ_u depend upon the grade of concrete and area of reinforcement which can be obtained from Table19 of IS code 456:2000

For M25 grade of concrete and percentage of steel = 0.25%

Ʈ_u = 0.36 N/mm²

Since, Ʈ_uc < Ʈ_v , so unsafe

Increase the depth of footing. Adopt 375 mm

Trial 2:

Shear force per meter, V_u = P_u,avg * B *{0.5(L-l) – d}

                                             = 224.76 * 2.2 * [0.5 (2.2 – 0.305) – 0.375]

                                             = 283.08 KN

Since the footing is square so the shear stress is same for both axis.

Nominal shear stress Ʈ_u = V_u /Bd

                                             = 283.08 / 2.2 * 0.375

                                             = 343 KN/m²

                                                            = 0.343 N/mm²

The nominal shear stress should be less than shear strength of the footing, that is

Shear strength Ʈ_uc = k Ʈ_c

K = 1 [For depth more than 300 mm]

For M25 and percentage of steel = 0.25%

Ʈ_u = 0.343 N/mm²

Since, Ʈ_uc > Ʈ_v , so safe

Step 7: Check for two way action of shear – punching shear

The critical section for two-way shear is taken at a distance d/2 away from the face of column.

P_u,max = 235.56 KN/m²

At critical section, ie at d/2 distance from edge of column

P_uy = 235.56 – (235.56 – 157.36)/ 2.2 * (2.2-0.305- 0.375)/2

= 208.54 KN/m²

P_uy,avg = ½ _* (P_u,max + P_uy)

               = (235.56 + 208.54)/2 = 222.05 KN/m²

Shear force per meter, V_u = P_u,avg [ L*B – (l+d)*(b+d)]

                                             = 222.05 * [2.2 * 2.2 – (0.305+0.375)* (0.305+0.375)]

                                             = 972.04 KN

Nominal shear stress Ʈ_u = V_u /b_o d

Where b₀ = perimeter of critical section = 2(l+b+2d) = 2* (0.305 +0.305 + 2 * 0.375) = 2.72 m

Ʈ_u = V_u /b_o d

= 972.04 / 2.72* 0.375

= 952.98 KN/m² =0.95 N/mm²

The nominal shear stress should be less than shear strength, that is

Ʈ_uc = 0.25 √f_ck = 0.25 * √ 25 = 1.25 N/mm²

Hence, safe in punching shear.

Step 8: Check for development length

The development length can be calculated using the clause 26.2.1 of IS code 456:2000,

Development length L_d = Փ * 0.87 f_y / 4τ_bd

Where, Փ = 20 mm = diameter of longitudinal bar of column

τ_bd = 1.4*1.6 = 2.25 = design bond stress given in clause 26.2.1.1.

Required development length L_d = Փ * 0.87 f_y / 4τ_bd

= 20 * 0.87* 415 / 4*2.25 = 802.33 mm

The calculated development length should be less than the available development length in the shorter side.

Available development length = L/2 – l/2 – side clear cover.

                                                            = 2200/2 – 305/2 – 65

                                                            = 882.5 mm > Req. L_d  , no anchorage required.

The value of side clear cover is normally taken as 50-75 mm

Step 10: Design Summary with arrangement of reinforcement.

The design summary isolated footing is as,

Size of footing = 2200 mm * 2200 mm

Effective depth of isolated footing = 375 mm

Reinforcement along both sides = 12 mm diameter bar @ 130 mm c/c

Overall depth of spread footing = effective depth + effective cover

                                                            = 375 + 65 = 440 mm

ALSO READ

DESIGN OF ISOLATED FOOTING