Modeling of infill masonry wall

 Masonry wall refers to the material crafted by a mason which may be brickwork or blockwork. Brick or block are normally in cuboidal shape which can be easily lifted. If the reinforcement are used in this types of masonry wall, then these wall are termed as reinforced-masonry wall, otherwise unreinforced masonry wall. Here we discuss about the modeling of infill masonry wall (unreinforced) . Infill refers that the wall is built in between the beam or columns.

In framed structure, the space in between the column is filled with the brick or concrete block wall with cement mortar. And the construction is for the security, privacy and for partition. The unreinforced infill-masonry wall is termed as non-load bearing member in framed structure. But in actual, the masonry wall also contribute in load transfer if the connection with the structural member (beam, column) is perfect.

The reason of not considering the infill-masonry wall as the structural member in framed structure is due to its low tensile strength. And even in moderate lateral force, normal diagonal cracks to heavy destruction occurs in masonry wall.

In structural design/analysis software like ETABS, SAP2000 or STAAD PRO, the structural member are only modeled neglecting the presence of infill masonry walls. Yes, equivalent weight of masonry wall is applied in the beam during load assigning. And also it gives satisfactory result during static condition. But such ignorance may cause huge effects during seismic activities.

As mentioned in Code IS 1893 (part 1): 2016 Clause 7.9,

RC Framed building with unreinforced masonry infill walls:

1. In RC building with moment resisting frames and unreinforced masonry infill walls, variation of storey stiffness and strength shall be examined along the height of the building considering in-plane stiffness and strength of URM infill walls. If storey stiffness and strength variation along the height of the building renders it to be regular as per table 6, the irregularity should be corrected in seismic zones III, IV and V. 

2. The estimation of in-plane stiffness and strength of URM infill walls shall be based on provision here under.

Modeling of URM infill masonry wall:

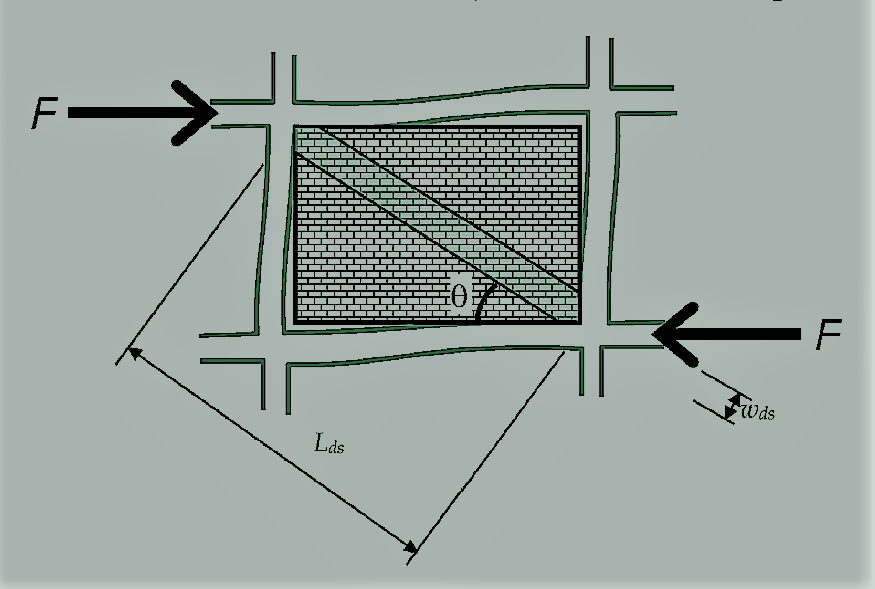
URM infill walls shall be modeled by using equivalent diagonal struts as below:

1. Ends of diagonals struts shall be considered to be pin-jointed to RC frame;
2. For URM infill walls without any opening, width w_ds of equivalent diagonal strut shall be taken as :

w_ds =0.175 α_h^-0.4 L_ds

                        where,

                                    α_h = h^’ ⁴√(E_m * t * sin2Ѳ / 4E_f * I_c *h)

where E_m and E_f are the moduli of elasticity of the materials of the URM infills and RC MRF,

I_c the moment of inertia of the adjoining column, t thickness of infill walls and Ө the angle of the diagonal struts with the horizontal;

The modulus of elasticity E_m (in MPa ) of masonry infill-wall shall be taken as :

                                         E_m = 550f_m

Where f_m is the compressive strength of masonry (in MPa) obtained as per IS 1905 or given by the expression:

                                         f_m = 0.433 f_b^0.64 f_mo^0.36

Where,

     f_b = compressive strength of brick, in MPa and

     f_mo = compressive strength of mortar, in MPa

Note : A simple and conservative expression of the width of equivalent strut was proposed as:

                             w_ds = 0.25 d_m

                       source: www.iitk.ac.in

EX. Modeling of infill masonry wall constructed with AAC block

 The modulus of elasticity E_m (in MPa ) of masonry infill-wall shall be taken as :

                                                E_m = 550f_m

Where f_m is the compressive strength of masonry (in MPa) obtained as per IS 1905 or given by the expression:

                                                f_m = 0.433 f_b^0.64 f_mo^0.36

                        f_b = compressive strength of brick, in MPa

                          = 3-4.5 N/mm² (AAC block)

Take f_b =3.5N/mm²

                        f_mo = compressive strength of mortar, in MPa           

                             = 10N/mm²  (M10)

On substituting,

                        f_m = 0.433 3.5^0.64 10^0.36

                                            = 2.2115 N/mm²

And E_m = 550f_m =550*2.2115

                           = 1216.3 MPa

For URM infill walls without any opening, width w_ds of equivalent diagonal strut shall be taken as :

w_ds =0.175 α_h^-0.4 L_ds

                        where,

                                    α_h = h^’  ⁴√(E_m * t * sin2Ѳ / 4E_f * I_c *h) 

where,

E_f = the moduli of elasticity of the materials of the RC MRF

    = 5000 √f_ck

    = 5000*√30

    = 27386.13 MPa

I_c = moment of inertia of adjoining column

    = b d³ / 12

    = 800 * 800³ /12

    = 3.4133 * 10¹⁰ mm⁴

t = thickness of masonry infill wall

  = 200mm (outer) and 150mm (inner)

h = clear height of URM infill wall between the top beam and bottom floor slab

   = 3.66 – 0.4 =3.26m = 3260mm

or = 4.27 – 0.4 =3.87m = 3870mm   

and Ө the angle of the diagonal struts with the horizontal

       Ө = tan^–(V/H)

For x-axis,

1.  floor height = 3.66m

Ө = tan^–(V/H)

   = tan^– (3.66/7.62)

   =25.65⁰

α_h = h^’  ⁴√(E_m * t * sin2Ѳ / 4E_f * I_c *h) 

    = 3260*  ⁴√((1216.3 * 200 * sin 2*25.65) / (4 *27386.13 * 3.1413 * 10¹⁰ * 3260))

    = 1.1485

w_ds =0.175 α_h^-0.4 L_ds

L_ds = length of equivalent diagonal struts

  = (V²+H²)^0.5

 = (3.66² + 7.62²)^0.5

 = 8.4534 m

w_ds =0.175 L_ds

      = 0.175 *1.1485^-0.4 *8453.4

      = 1449.3 mm

•  floor height = 4.27m

Ө = tan^–(V/H)

   = tan^– (4.27/7.62)

   =29.26⁰

α_h = h^’     

    = 3870*       

    = 1.339

w_ds =0.175 L_ds

L_ds = length of equivalent diagonal struts

  = (V²+H²)^0.5

 = (4.27² + 7.62²)^0.5

 = 8.7348 m

w_ds =0.175 L_ds

      = 0.175 *1.339^-0.4 *8734.8

      = 1360 mm

ALSO READ :

DESIGN OF SHEAR WALL

DESIGN OF BASEMENT WALL