Table of Contents
One way slab:
One way slab are the slab that are supported on two parallel sides carrying loads by flexure in the direction perpendicular to the support and ratio of longer to shorter span greater than 2. Here we discuss about numerical of one-way slab, both simply supported and continuous. The design procedure of one way slab is already discussed under topic of ONE WAY SLAB DESIGN before.
1. Numerical of one-way slab – Simply supported:
Example: Design a simply supported reinforced concrete slab for a room of clear dimension of 3.81 m * 10.02 m. The slab is supported all around wall of width 300 mm. The slab has to carry live load 3 KN/m2 and floor finish and partition load of 1.5KN/m2. Use M30 concrete and Fe 500 steel.
The numerical of one-way slab – simply supported is explained in step wise procedure below:
Step 1. Calculate aspect ratio and determine either it is one-way or two-way slab.
Aspect ratio = longer span / shorter span
= 10.02/3.81
= 2.63
Since greater than 2, it is one-way slab.
Step 2. Determine the minimum thickness of slab from serviceability criteria of deflection control.
[As it is already discussed in preliminary design of slab, you can CLICK HERE go there for further details.]
Assume, shorter span/ depth = 28 [From IS 456:2000 clause 24.1]
Effective depth = 3810/28 = 136mm
Assume, diameter of bar = 10mm and clear cover = 15mm
So, overall depth of slab = effective depth + clear cover + half diameter of bar
= 136 +15 + 5
= 156mm
For construction easiness take overall depth 150mm and check.
So, effective depth = 150 – 15 – 5 = 130 mm
Step 3. Calculate the effective span of slab from IS 456 clause 22.2 which is least of following values
- Center to center of supports or clear span + width of support
- Clear span + effective depth of slab
Since width of support (ie. 300mm) is greater than effective depth of slab ( ie. 130mm) so, the point (b) gives least value.
Effective span of slab along shorter side = Clear span + effective depth of slab
= 3810 + 130 = 3940mm
Effective span of slab along longer side = Clear span + effective depth of slab
= 1020 + 120 = 1140 mm
[Reinforcement in longer span lies above main reinforcement so effective depth is less by a diameter of bar]
Step 4. Determine the total factored load due to live and dead load considering 1m wide strip.
Self-weight of slab = depth of slab * unit width * unit weight of RCC
= 0.15 * 1 * 25 = 3.75 KN/m
Dead load due to floor finish and partition = 1.5 * 1 = 1.5 KN/m
Live load on slab = 3 * 1 = 3 KN/m
Total load = 3.75 + 1.5 + 3 = 8.25 KN/m
Factored load (w) = 1.5 * total load = 1.5 * 8.25 = 12.375 KN/m
Step 5. Calculate the factored design moment Mu and factored design shear force Vu.
Factored moment Mu = w l² / 8 = 12.375 * 3.94² / 8
= 16 KN-m
[l used in the formula denotes effective span along shorter span due to its load transfer mechanism]
Factored shear force Vu = w l / 2 = 12.375 * 3.94 / 2 = 24.4 KN
Step 6. Check the thickness of slab.
The thickness of slab is derived for calculated value of factored moment.
Mu = Mu,lim = 0.36 fck b xu [d – 0.42 xu]
For Fe 500, xu/d = 0.46 [from IS 456:2000 clause 38.1]
Therefore, Mu = Mu,lim = 0.1336 fck b d²
[Since, width of slab b is taken as 1m ]
16 * 106 = 0.1336 * 30 * 1000 * d²
d = 63.18mm < 130mm, OK
Step 7. Determine the area and spacing of main reinforcement.
The area can be calculated from given formula;
Mu = 0.87 fy As [d – fy As/ fck b]
16 * 106 = 0.87 * 500 * As [130 – 30 * As / 30*1000]
As = 283.55 mm²
Since diameter of bar = 10 mm
Spacing of bar = area of a bar * width of strip / area of reinforcement required
= 78.54 * 1000 / 283.55 = 277 mm
The spacing of main reinforcement bar should not be more than 3 times the effective depth of solid slabs or 300 mm whichever is smaller.
3d = 3* 130 = 390mm
So, provide spacing of 250 mm
Area provided = 78.54 * 1000 / 250 = 314.16 mm²
And the minimum area of main steel reinforcement is equal to 0.12% of bD.
Min. area required = 0.12* 1000 * 150 / 100 = 180 mm² < 314.16 mm² (area provided), Ok
Step 7. Check the adequacy of depth from deflection control criteria.
For deflection control criteria, using IS 456:2000 clause 23.2.1
For modification factor for tension reinforcement,
fs = 0.58 fy * area required / area provided
= 0.58 * 500 * 283.55/314.6
= 261.4
Steel percentage = 314.16 *100/ 1000*150 = 0.21 %
Using graph,
Modification factor = 1.5
Hence allowable l/d = 20 * 1.5 = 30 > 28 (assumed), OK
Step 8. Check for shear
For one-way slab, it would not be a bad practice to check for shear.
Ⴀu = Vu/bd = 24.4 *1000/1000*130 = 0.19 N/mm²
Assume tension steel in support = percent provided in mid span / 2
= 0.21/2 = 0.105%
From table 19, IS 456:2000
Ⴀc = 0.29 N/mm² > 0.19 N/mm²
Hence, slab is safe in shear, even without shear enhancement using factor k
Step 9. Calculate the distribution reinforcement.
From IS 456:2000 clause 26.5.2.1; the distribution reinforcement should be provided 0.12% of b D if high strength deformed bar or 50% of main reinforcement whichever is greater.
Area of distribution bar = 0.12% of bD = 0.12* 1000 * 150 / 100 = 180 mm²
Since diameter of bar = 10 mm
Spacing of bar = area of a bar * width of strip / area of reinforcement required
= 78.54 * 1000 / 180 = 436.2 mm
The spacing of distribution bar should not be greater than 5 times the effective thickness of slab or 450mm whichever is smaller.
5d = 5 * 130 = 650 mm
So, provide spacing of distribution bar equal to 400 mm
Step 10. Check for development length
From IS 456:2000 clause 26.2.1
The development length is given by
Ld = 0.87 fy Փ / 4Ⴀbd
= 0.87 * 500 * 10 / 4 * 1.5 * 1.6
=453.125 mm
From clause 26.2.3.3a of code IS 456:2000, embedded length into support > Ld/3
Ld/3 = 151 mm
Length of embedment on support = width of support – side clear cover = 300 – 30 = 270 mm > Ld/3, OK
After the completion of numerical of one-way slab – simple supported, we have to show the arrangement of reinforcement. The reinforcement can be arranged as mentioned on code as shown;
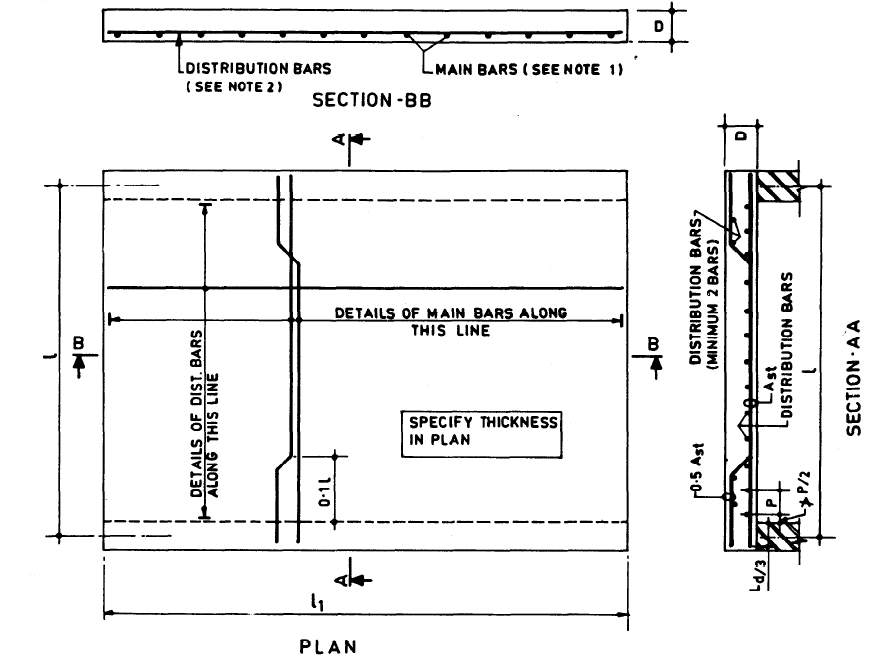
Continuous slab design:
There is negative moment at support and positive moment at mid-span of continuous slab. For the design and construction easiness, design is usually made for maximum bending and maximum shear force which is at the supports. For finding the moments and shear force at critical sections, the IS 456:2000 Table 12 and 13 are used.
The maximum moment is at the support next to end support which is equal to,
Mmax= (DL/12 + LL/9) * l²
And maximum shear force is at outer of first interior which is equal to ,
Vmax = (0.6 DL + 0.6 LL) * l
Where l is the shorter span
DL = dead load and LL = live load
NUMERICAL OF ONE-WAY SLAB – CONTINUOUS
Example: Design a continuous reinforced concrete slab for room of 10.02 m wide and 19.05 m long. The slab is supported on RCC beam of width 300 mm at 3.81 intervals. The slab has to carry live load 3 KN/m2 and floor finish and partition load of 1.5KN/m2. Use M30 concrete and Fe 500 steel.
The numerical of one-way slab – continuous is explained in step wise procedure below:
Step 1. Calculate aspect ratio and determine either it is one-way or two-way slab.
Aspect ratio = longer span / shorter span
= 10.02/3.81
= 2.63
Since greater than 2, it is one-way slab.
Step 2. Determine the minimum thickness of slab from serviceability criteria of deflection control.
[As it is already discussed in PRELIMINARY DESIGN OF SLAB]
Assume, shorter span/ depth = 32 [From IS 456:2000 clause 24.1]
Effective depth = 3810/32 = 119mm, adopt 120mm
Assume, diameter of bar = 10mm and clear cover = 15mm
So, overall depth of slab = effective depth + clear cover + half diameter of bar
= 120 +15 + 5
= 140mm
Step 3. Calculate the effective span of slab from IS 456 clause 22.2 which is least of following values
- Center to center of supports or clear span + width of support
- Clear span + effective depth of slab
Since width of support (ie. 300mm) is greater than effective depth of slab ( ie. 130mm) so, the point (b) gives least value.
Effective span of slab along shorter side = Clear span + effective depth of slab
= 3810 + 120 = 3930mm
Effective span of slab along longer side = Clear span + effective depth of slab
= 1020 + 110 = 1130 mm
[Reinforcement in longer span lies above main reinforcement so effective depth is less by a diameter of bar]
Step 4. Determine the total factored load due to live and dead load considering 1m wide strip.
Self-weight of slab = depth of slab * unit width * unit weight of RCC
= 0.14 * 1 * 25 = 3.5 KN/m
Dead load due to floor finish and partition = 1.5 * 1 = 1.5 KN/m
Live load on slab = 3 * 1 = 3 KN/m
So, DL = 5 KN/m
LL = 3 KN/m
Step 5. Calculate the factored design moment Mu and factored design shear force Vu.
From table 12 of IS456:2000, maximum moment occurs at support next to end support and given by,
Mu = 1.5 (DL * l² /10 +LL * l² /9)
= 1.5 (5 * 3.93²/10 + 3* 3.93²/9)
= 18.53 KN-m
[l used in the formula denotes effective span along shorter span due to its load transfer mechanism]
Again from table 13 of IS456:2000,
The maximum shear force occurs at the outer side of the support next to the end support and is given by, Factored shear force Vu = 1.5 * ( 0.6 * DL * l + 0.6 LL * l)
= 1.5 * (0.6 * 5 * 3.93 + 0.6 * 3 * 3.93) = 28.3 KN
Step 6. Check the thickness of slab.
The thickness of slab is derived for calculated value of factored moment.
Mu = Mu,lim = 0.36 fck b xu [d – 0.42 xu]
For Fe 500, xu/d = 0.46 [from IS 456:2000 clause 38.1]
Therefore, Mu = Mu,lim = 0.1336 fck b d²
[Since, width of slab b is taken as 1m ]
18.53 * 106 = 0.1336 * 30 * 1000 * d²
d = 68mm < 120mm, OK
Step 7. Determine the area and spacing of main reinforcement.
The area can be calculated from given formula;
Mu = 0.87 fy As [d – fy As/ fck b]
18.53 * 106 = 0.87 * 500 * As [120 – 30 * As / 30*1000]
As = 356 mm²
Since diameter of bar = 10 mm
Spacing of bar = area of a bar * width of strip / area of reinforcement required
= 78.54 * 1000 / 356 = 220.62 mm
The spacing of main reinforcement bar should not be more than 3 times the effective depth of solid slabs or 300 mm whichever is smaller.
3d = 3* 120 = 360mm
So, provide spacing of 200 mm
Area provided = 78.54 * 1000 / 200 = 392.7 mm²
And the minimum area of main steel reinforcement is equal to 0.12% of bD.
Min. area required = 0.12* 1000 * 140 / 100 = 168 mm² < 392.7 mm² (area provided), Ok
Step 7. Check the adequacy of depth from deflection control criteria.
For deflection control criteria, using IS 456:2000 clause 23.2.1
For modification factor for tension reinforcement,
fs = 0.58 fy * area required / area provided
= 0.58 * 500 * 356 / 392.7
= 262.9
Steel percentage = 392.7 *100/ 1000*140 = 0.28 %
Using graph,
Modification factor = 1.4
Hence allowable l/d = 26 * 1.4 = 36.4 > 32 (assumed), OK
Step 8. Check for shear
For one-way slab, it would not be a bad practice to check for shear.
Ⴀu = Vu/bd = 28.3 *1000/1000*120 = 0.236 N/mm²
Assume tension steel in support = percent provided in mid span / 2
= 0.28/2 = 0.14%
From table 19, IS 456:2000
Ⴀc = 0.29 N/mm² > 0.236 N/mm²
Hence, slab is safe in shear, even without shear enhancement using factor k
Step 9. Calculate the distribution reinforcement.
From IS 456:2000 clause 26.5.2.1; the distribution reinforcement should be provided 0.12% of b D if high strength deformed bar or 50% of main reinforcement whichever is greater.
Area of distribution bar = 0.12% of bD = 0.12* 1000 * 140 / 100 = 168 mm²
Since diameter of bar = 10 mm
Spacing of bar = area of a bar * width of strip / area of reinforcement required
= 78.54 * 1000 / 168 = 467.5 mm
The spacing of distribution bar should not be greater than 5 times the effective thickness of slab or 450mm whichever is smaller.
5d = 5 * 130 = 650 mm
So, provide spacing of distribution bar equal to 400 mm
After the completion of numerical of one-way slab – continuous slab, we have to show the arrangement of reinforcement. The arrangement should be done as explained on the codes.
ALSO READ

