Design of column

Column

Column is the vertical compression member of the building with or without bending moment. In normal residential and commercial building, the height of column is about 3 – 4 m. Since the column is supported with fixed end support, the effective length of column is equal to 0.65 times the unsupported length. Most of the column of residential, institutional and commercial building are short column because their slenderness ratio is lower than 12. Design steps of short column

Design example of column

Design a column of an institutional whose unsupported length is 3.66 m. Grade of concrete = 30MPa and grade of steel = 500 N/mm². Thickness of slab = 130 mm and size of all beam = 400 mm* 600mm. Assume all suitable data necessary.

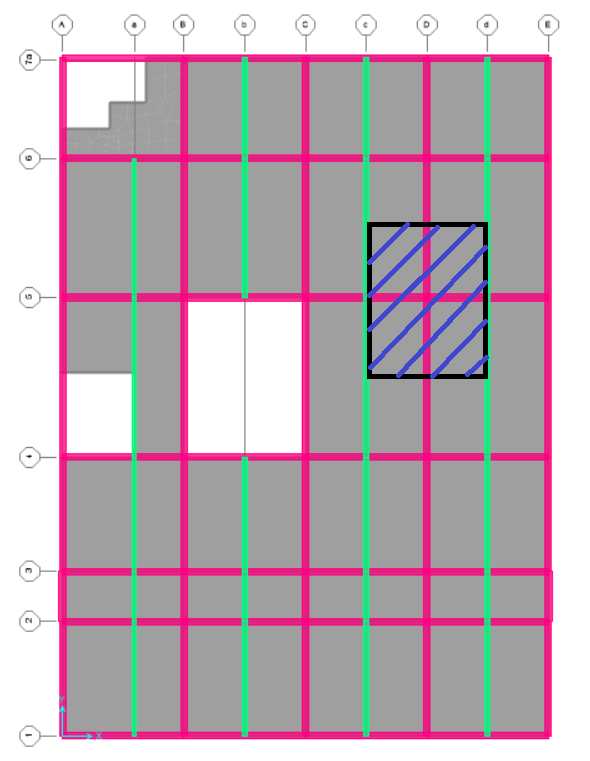
All the dimension are given in architectural plan below.

The figure of SAP2000 shows the load distribution of that column which we go for design. It also shows primary and secondary beam present in the building. The light green color line is secondary beam whereas the pink color line is primary beam. The hatched area is that area of slab whose load is taken by that column present in center.

Step 1: Preliminary design of column

               The initial sizing of column is already discussed in preliminary design of column. Click here for details.

Size of column from preliminary design = 800mm * 800mm

Step 2: Calculate effective length of column and check for long/short column

The effective length of column is determined based on the end supports and the sway/no sway condition. Depending on the ratio of the effective length to the least lateral dimension of the column, the column is classified as either a short column or a long column. If the ratio of its effective length to its least lateral dimension is less than 12, the column will be short column.

Assume the column is in no sway condition, the effective length can be taken as 0.65L where L is the unsupported height of the column.

Effective length ( l ) = 0.65 L

                                      = 0.65 * 3.66 = 2.379 m

Slenderness ratio (λ) = l/b = 2.379 / 0.8 = 2.97; so the column is short column.

Step 3: Calculate minimum eccentricity along both axes

The eccentricity of the column can be calculate by using code IS 456:2000 of clause 25.4

e_min = unsupported length / 500 + lateral dimension / 30

= 3600/500 + 800/30 = 33.86 mm ≥ 20mm

Permissible eccentricity = 0.05 * lateral dimension = 0.05 * 800 = 40mm > e_min

 Step 4: Calculate factored axial force and bending moment on the column

The value of axial force and bending moment can be extracted from the any structural software like ETABS, SAP2000 or STAAD PRO. Here the data used is from SAP2000 but you can also use any other software.

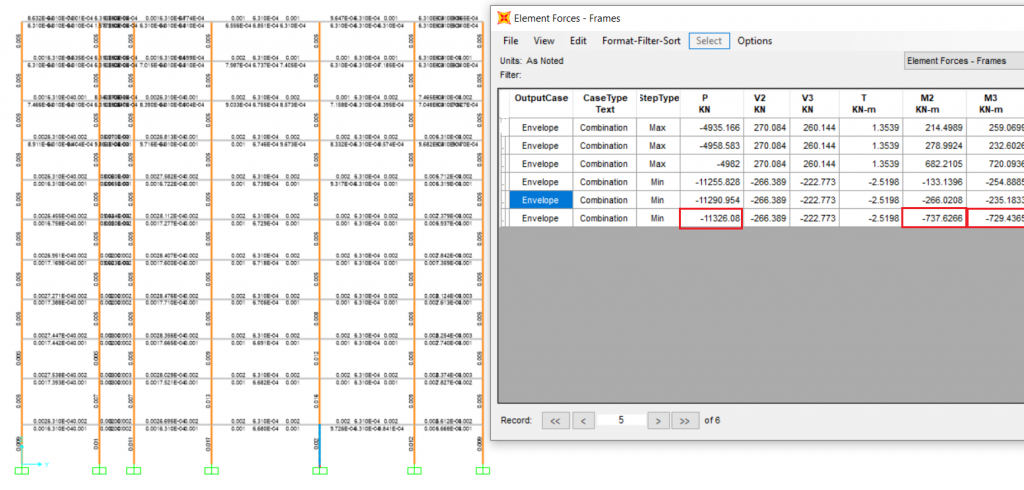
Axial force P_u= 11326.08 KN > 0.1 f_ck bD [ 0.1 * 30 * 800 * 800 = 1920000 N = 1920 KN],  Ok

Bending moment,

M_ux = 737.64 KN-m > P_u * e_min  [ 11326.08 * 33.86/1000 = 383.5 KN-m]

M_uy = 729.44 KN-m > P_u * e_min  [ 11326.08 * 33.86/1000 = 383.5 KN-m]

Step: 4 Calculate the ratio of effective cover to lateral dimension

               The lateral dimension (b, D) is derived from the preliminary design of column.

               b= D = 800mm

 Assume effective cover d’ = 60 mm

The ratio of effective cover to lateral dimension are

d’/b = d’/D = 60 / 800 = 0.075

Step 5: calculate p/f_ck and P_u/f_ckbD

Where, p = percentage of steel

Either we can directly assume the percentage of steel [ 2%] or we have to calculate percentage of steel is calculated for given size of column adopted from preliminary design. The percentage of longitudinal reinforcement can be calculated as,

P_u = 0.4 f_ck A_c + 0.67 f_y A_sc

Where, P_u = factored axial load

               f_ck & f_y  = characteristic strength of concrete and steel

               A_c & A_sc = Area of concrete and steel

Here A_sc & A_c are expressed in percentage of gross area.

P_u = 0.4 f_ck A_g (1-0.01p) + 0.67 f_y A_g 0.01p

11326.08 *1000 = 0.4 *30 * 800*800 (1+0.01p) + 0.67 * 500 * 800 * 800 * 0.01p

 P = 1.764%

Adopt 2 % for I^st trial

[Note: Since the reinforcement also have to resist the bending moment acting on the column so assume steel should be greater than that from the above formula]

Step: 6 Calculate M_ux1 and M_uy1

M_ux1 = M_{uy1 ,} since the column is square.

Since the d’/b = d’/D = 0.075 so take chart 47 and 48 for reinforcement distributed equally on four sides

P_u/f_ck bD = 11326.08 *1000 / 30 * 800 * 800 = 0.59

p/f_ck = 2/30 = 0.067

From chart 47 of SP16, [ for f_y =500 N/mm² , d’/b =0.05]

M_u / f_ck b D² = 0.035

From chart 48 of SP16, [ for f_y =500 N/mm² , d’/b =0.1]

M_u / f_ck b D² = 0.04

So from interpolation, for d’/b =0.075

M_u / f_ck b D² = 0.0375

M_u = 0.0375 * 30 * 800 * 800² = 576000000 N-mm = 576 KN-m

From clause 39.6 of IS code 456:2000,

The value of α_n can be calculated from the relation

α_n = 0.667 + 1.661 * P_u/P_z

where, P_z = 0.45 f_ck A_c + 0.75 f_y A_sc

               = 0.45 * 30 * 0.98 * 800* 800 + 0.75 * 500 * 0.02 * 800 * 800

               = 13267200 N = 13267.2 KN

So, α_n = 0.667 + 1.661 * P_u/P_z

               = 0.067 + 1.661 * 11326.08/13267.2 = 1.485

 Step 7: Check for safe

For the design to be safe check the equation given in 39.6 of IS 456:2000.

 [M_ux / M_ux1] ^α_n + [ M_uy / M_uy1] ^α_n

= [737.36 / 576 ]^1.485 + [ 729.44 / 576 ]^1.485

               = 2.863 > 1

So go for next trial.

Trial 2

Adopt percentage of steel = 2.7%

p/f_ck = 2.7 /30 = 0.09

P_u/f_ck bD = 11326.08 *1000 / 30 * 800 * 800 = 0.59

From chart 47 of SP16, [ for f_y =500 N/mm² , d’/b =0.05]

M_u / f_ck b D² = 0.085

From chart 48 of SP16, [ for f_y =500 N/mm² , d’/b =0.1]

M_u / f_ck b D² = 0.08

So from interpolation, for d’/b =0.075

M_u / f_ck b D² = 0.0825

M_u = 0.0825 * 30 * 800 * 800² = 1267200000 N-mm = 1267.2 KN-m

From clause 39.6 of IS code 456:2000,

The value of α_n can be calculated from the relation

α_n = 0.667 + 1.661 * P_u/P_z

where, P_z = 0.45 f_ck A_c + 0.75 f_y A_sc

               = 0.45 * 30 * 0.973 * 800* 800 + 0.75 * 500 * 0.027 * 800 * 800

               =14886720 N = 14886.72 KN

So, α_n = 0.667 + 1.661 * P_u/P_z

               = 0.067 + 1.661 * 11326.08/14886.72 = 1.33

 Check for safe

For the design to be safe check the equation given in 39.6 of IS 456:2000.

 [ M_ux / M_ux1] ^α_n +[ M_uy / M_uy1] ^α_n

= [ 737.36 / 1267.2 ]^1.33 + [ 729.44 / 1267.2 ]^1.33

               = 0.966 ≤ 1 Ok

Note: The design will be more economical if the value of [ M_ux / M_ux1] ^α_n +[ M_uy / M_uy1] ^α_n become closely equal to 1.

  Step 8: Calculate the number of longitudinal bar

Area of longitudinal bar A_sc = percentage of steel * size of column

                                             = 0.027 * 800 * 800 = 17180 mm²

Assume the diameter of bar = 28 mm

Area of a bar = pi * 28²/4 = 615.44 mm²

Number of bar = Area of longitudinal bar A_sc / area of a reinforcement bar

                              = 17180 / 615.44 = 27.9 nos

Provide 28 numbers of longitudinal reinforcement bar.

Step: 9 Calculate lateral ties

1. The diameter of lateral ties shall be greater than

= 1/4^th of diameter of longitudinal bar = 28/4 =7 mm

= 6mm

2. The spacing of lateral ties shall be least of following

= least lateral dimension = 800 mm

= 16 * diameter of longitudinal bar = 448 mm

=300mm

So provide lateral ties of diameter 8 mm @ 300 c/c spacing.

Step: 10 Design summary with diagrammatic arrangement.

 Size of column = 800 mm * 800 mm

 Longitudinal bar = 28 number of 28mm diameter bar

Transverse bar = 8 mm @ 300mm c/c spacing

The arrangement of longitudinal reinforcement is as shown in figure,

The arrangement of transverse reinforcement should be done as mentioned in IS 13920:2016 clause 7.4